Произведение (теория категорий)
Произведение двух или более объектов — это обобщение в теории категорий таких понятий, как декартово произведение множеств, прямое произведение групп и произведение топологических пространств. Произведение семейства объектов — это в некотором смысле самый общий объект, имеющий морфизмы во все объекты семейства.
Определение
[править | править код]Пусть задано — индексированное семейство (не обязательно различных) объектов категории . Объект категории вместе с семейством морфизмов является произведением семейства объектов , если для любого объекта и любого семейства морфизмов существует единственный морфизм , для которого следующая диаграмма:

коммутативна для каждого (то есть ). Морфизмы называются каноническими проекциями.
Приведенное определение равносильно следующему:
Объект вместе с семейством проекций является произведением семейства объектов тогда и только тогда, когда для любого объекта отображение
Произведение двух объектов обычно обозначают , при этом диаграмма принимает вид
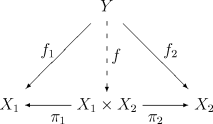
Морфизм при этом иногда обозначается .
Единственность результата операции можно альтернативно выразить как равенство , верное для любых .[1]
Примеры
[править | править код]- В категории множеств категорное произведение совпадает с декартовым.
- В категории топологических пространств произведению пространств соответствует пространство, носитель которого является декартовым произведением носителей сомножителей, а топология определяется как произведение их топологий.
- В категории групп произведение групп определяется как их прямое произведение.
- В категории проективных многообразий категорное произведение можно задать при помощи вложения Сегре.
- Частично упорядоченное множество может рассматриваться как категория, в которой морфизм из в существует тогда и только тогда (по определению), когда (причём между двумя объектами не может быть более одного морфизма). При этом произведением семейства линейно упорядоченных объектов является их наибольшая нижняя грань, а копроизведением — наименьшая верхняя грань.
Свойства
[править | править код]- Если произведение объектов существует, то оно единственно с точностью до изоморфизма.
- Коммутативность:
- Ассоциативность:
- Если в категории существует терминальный объект , то
- Приведённые выше свойства формально сходны со свойствами коммутативного моноида. Более точно, категория, в которой определено произведение любых двух объектов и имеется терминальный объект, является симметричной моноидальной категорией.
Дистрибутивность
[править | править код]В общем случае существует канонический морфизм , где плюс обозначает копроизведение объектов. Это следует из существования канонических проекций и вложений и из коммутативности следующей диаграммы:
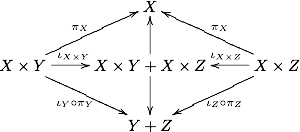
Свойство универсальности для гарантирует при этом существование искомого морфизма. Категория называется дистрибутивной, если в ней этот морфизм является изоморфизмом.
Матрица преобразований
[править | править код]Любой морфизм
порождает множество морфизмов
задаваемых по правилу и называемых матрицей преобразования. Обратно, любая матрица преобразования задаёт единственный соответствующий морфизм Если в категории существует нулевой объект то для любых двух объектов существует канонический нулевой морфизм: В этом случае матрица преобразования , задаваемая по правилу
называется единичной матрицей.
- Пример
В категории конечномерных векторных пространств копроизведение пространств совпадает с их произведением и является их прямой суммой. В этом случае категорное и обычное определение матрицы преобразования совпадают, так как любое конечномерное пространство можно разложить в прямую сумму одномерных, а также и в прямое произведение одномерных. Различие состоит в том, что в категорном определении элементы матрицы — это преобразования одномерного пространства в одномерное, тогда как в обычном определении в этих одномерных пространствах выбраны базисы и можно указывать только координату образа базисного вектора пространства-прообраза в базисе пространства-образа.
См. также
[править | править код]- Копроизведение — понятие, двойственное произведению.
- Декартово замкнутая категория
Примечания
[править | править код]- ↑ Lambek J., Scott P. J. Introduction to Higher-Order Categorical Logic. — Cambridge University Press, 1988. — С. 304.
Литература
[править | править код]- Букур И., Деляну А. Введение в теорию категорий и функторов = Introduction to the theory of categpries and functors. — М.: Мир, 1972. — С. 39. — 259 с.
- Маклейн С. Категории для работающего математика. — М.: Физматлит, 2004 [1998].
- Жаринов В. В. Некоторые алгебро-геометрические методы в математической физике. — С. 8. — 82 с.




































